[ad_1]
C++14 has numerous options that assist functional-style design. By “functional-style” I imply heavy use of higher-order features (features that take different features as arguments). Very often arguments to the higher-order features are lambdas (closures, to be exact). With automated return sort deduction for regular features, writing higher-order perform turns into very straightforward and seamless in C++14.
This time, I’ve chosen a “text-book” instance to indicate you the ability of C++14: Composable Knowledge Mills
What’s a Generator?
A Generator<T> produces values of sort T randomly. There may be already a random quantity generator outlined within the C library: random(). It produces lengthy ints.
We are able to use this primary generator to create higher-level mills, similar to bool, character, floating level numbers, and many others. Even random sequence and construction mills are doable.
However first, lets add some construction across the C library perform in order that we will compose mills.
#embrace <cstdlib>
struct RootRandomGen
{
lengthy int operator () () const
{
return random();
}
};
RootRandomGen is a quite simple function-object that when referred to as produces a random quantity between 0 and RAND_MAX.
Let’s create a Generator template from which we will create different mills.
template <class T, class GenFunc>
class Gen
{
GenFunc genfunc;
public:
express Gen(GenFunc func)
: genfunc(std::transfer(func))
{ }
T generate()
{
return genfunc();
}
};
The Gen class template permits us to move any function-object or closure and a make a “generator” out of it. In fact, the perform should not take any arguments and should produce a worth.
To simplify creation of Mills from simply lambdas, we create a helper manufacturing unit perform. That is the place the ability of C++14 begins changing into obvious.
template <class GenFunc>
auto make_gen_from(GenFunc&& func)
{
return Gen<decltype(func()), GenFunc>(std::ahead<GenFunc>(func));
}
make_gen_from is a higher-order perform that takes a closure as an argument and creates a Gen<T> object. GenFunc is the kind of the closure. The kind T is deduced utilizing decltype(func()), which is C++14 syntax to say no matter the kind of the return worth of func is. Remainder of it’s perfect-forwarding of the func argument to the Gen<T> object.
To create many extra mills, similar to for bool, char, string, and many others, a perform like make_gen<T> is likely to be fairly helpful. So, let’s add one.
template <class T>
auto make_gen();
template <>
auto make_gen<lengthy int>()
{
return make_gen_from(RootRandomGen());
//return make_gen_from([]() { return random(); });
}
The lengthy int generator merely makes use of the “Root” generator. Alternatively, RootRandomGen could be outlined in-place utilizing a lambda as proven above. I.e., RootRandomGen is superfluous.
Let’s check what we have to this point.
void init_random()
{
time_t t;
time(&t);
srandom(t);
}
int fundamental(void)
{
init_random();
auto gen = make_gen<lengthy int>();
std::cout << gen.generate(); // count on a random worth.
}
We are able to create many extra mills by explicitly specializing make_gen for numerous sorts. However earlier than we do that allow’s observe the core properties of Gen<T>.
The Generator<T> Functor
In purposeful programming literature, Gen<T> is a functor, which suggests you possibly can “map over it”. I.e., you possibly can write a perform named map that takes a generator and a perform and returns one other generator that applies the perform to the values generated by the argument generator. It is a lot simpler to have a look at code.
template <class Gen, class Func>
auto map (Gen gt, Func func)
{
return make_gen_from([gt, func]() {
return func(gt.generate());
});
}
First, the lambda captures gt and func by worth. When referred to as, it first generates a worth from gt and passes it to the perform and easily returns the worth produced by the perform. We have already seen that make_gen_from converts any lambda (with proper signature) to a generator. So we now have a really general-purpose facility to create arbitrarily many mills just by passing features to map.
Let’s take a look at an instance.
int fundamental(void)
{
init_random();
auto gen = make_gen<lengthy int>();
auto boolgen = map(gen, [](lengthy int i) { return bool(i % 2); });
std::cout << std::boolalpha << boolgen.generate(); // count on a random boolean.
}
The one downside, nonetheless, is that it doesn’t work.
The issue is that Gen<T> is designed to assist stateful mills that may mutate state between two successive calls to generate. That is why the generate perform just isn’t const. However the lambda within the map perform is by default const. Due to this fact, gt can also be const, which prevents us from calling gt.generate() as Gen<T>::generate() is a non-const perform.
The answer is to make the lambda in map perform mutable. With that, this system compiles however there are extra issues that may be improved about map.
First, gt and func arguments are handed by worth and the lambda captures them by worth. That could be probably fairly wasteful. We are able to enhance effectivity through the use of excellent forwarding. Including excellent forwarding, nonetheless, provides numerous noise to the in any other case easy map perform. This noise has develop into my pet peeve concerning functional-style programming in C++14.
template <class Gen, class Func>
auto map (Gen&& gt, Func&& func)
{
return make_gen_from([gt=std::forward<Gen>(gt),
func=std::forward<Func>(func)]() mutable {
return func(gt.generate());
});
}
I feel this map perform is a well-behaved citizen of the C++14 world. It is utilizing the generalized lambda seize syntax and perfect-forwarding together.
Utilizing this map perform is barely awkward as a result of it is a free perform. To assist extra fluent type of API, I wish to “improve” the map perform to the Gen<T> class. As I stated earlier than, each generator helps mapping. So this is the brand new Get<T> template.
template <class T, class GenFunc>
class Gen
{
GenFunc genfunc;
public:
express Gen(GenFunc func)
: genfunc(std::transfer(func))
{ }
T generate()
{
return genfunc();
}
template <class Func>
auto map (Func&& func)
{
return make_gen_from([gt=*this,
func=std::forward<Func>(func)]() mutable {
return func(gt.generate());
});
}
};
Observe that map makes a full copy of this within the lambda so that each generator turns into self-sufficient.
We are able to create numerous different mills utilizing the built-in map perform. For example, an think about Gen<int> under.
template <>
auto make_gen<int>()
{
return make_gen<lengthy int>().map([](lengthy int i) { return static_cast<int>(i); });
}
A spread generator that produces a random worth within the specified vary could also be created as follows. Like within the iterator semantics, hello is one previous the fascinating vary.
template <class Integer>
auto make_range_gen(Integer lo, Integer hello)
{
return make_gen<lengthy int>().map(
[lo, hi](lengthy int x) { return static_cast<Integer>(lo + x % (hello - lo)); });
}
Utilizing the vary generator, a generator for uppercase characters is kind of easy.
auto uppercase_gen = make_range_gen('A', 'Z'+1);
std::cout
Combinators
Many extra helper features could be added to the Gen<T> class that produce new mills from argument mills. In purposeful literature they're referred to as combinators.
This is the zip2 combinator: Zip works similar to a zipper. It takes 2 mills and produces one other generator that mixes the values generated by the argument mills. To mix the values, it wants a perform that accepts two arguments and return a worth. The consumer should present the perform.
template <class T, class GenFunc>
class Gen
{
// ....
template <class UGen, class Zipper2>
auto zip2(UGen&& ugen, Zipper2&& func)
{
return this->map(
[ugen=std::forward<UGen>(ugen),
func=std::forward<Zipper2>(func)](auto&& t) mutable {
return func(std::ahead<decltype(t)>(t), ugen.generate());
});
}
};
auto uppergen = make_range_gen<char>('A', 'Z'+1);
auto lowergen = make_range_gen<char>('a', 'z'+1);
auto pairgen =
uppergen.zip2(lowergen,
[](char up, char low) { return std::make_pair(up, low); });
The instance above reveals how a pair of random characters could be produced by zipping an uppercase generator with a lowercase generator. The zipper perform merely constructs the pair from two characters. Alternatively, &std::make_pair<char, char> would have been adequate.
The zip2 perform seems to be considerably extra verbose than a comparable implementation in most different languages that assist lambdas. A number of code is dedicated to perfect-forwarding of arguments, which is kind of mandatory for extremely composable libraries similar to this one. We'll see later that C++ compilers are sensible sufficient to inline the call-chain fully.
One other instance of zip is string generator. A string generator zips a bool generator and int generator the place the bool worth signifies whether or not string is empty or not and int generator determines the size of the string. In fact, string generator additionally wants a char generator to populate the string. This is a method of doing it.
template <>
auto make_gen<std::string>()
{
auto char_gen = make_range_gen(32, 127); // printable characters.
auto length_gen = make_range_gen(1, 256);
return make_gen<bool>().zip2(
length_gen,
[char_gen](bool empty, int size) mutable {
std::string str;
if(!empty)
{
str.reserve(size);
for(int i = 0; i < size; ++i)
str.push_back(char_gen.generate());
}
return str;
});
}
There are numerous extra combinators. The single generator would at all times produce the identical worth. The oneOf generator selects one of many parts from a given array non-deterministically. Lastly, the amb combinator will use of the 2 enter combinators to provide worth. This is a few them.
template <class T>
auto make_single_gen(T&& t)
{
return make_gen_from([t=std::forward<T>(t)]() { return t; });
}
template <class T>
auto make_oneof_gen(std::initializer_list<T> listing)
{
return make_range_gen(0ul, listing.measurement()).map([list](int idx) { return *(listing.start()+idx); });
}
Stateful Mills
The examples we have seen to this point are stateless mills. I.e., between two successive calls to generate, no state is up to date. Let's take a look at a stateful generator: fibonacciGen. This generator should keep not less than two integers (a and b) for its computation.
auto fiboGen()
{
int a = 0;
int b = 1;
return make_gen_from([a, b]() mutable {
int c = a;
a = b;
b = c+b;
return c;
});
}
The Price of Purposeful Design
It's fairly attention-grabbing how advanced mills could be created from easy mills. However is there a value to this excessive degree of abstraction? Is the code as quick as it may be?
Listed below are two completely different algorithmically an identical implementations of bool generator. The explanation I selected this algorithm as a result of I wished make use of zip2, which in flip makes use of map. I wished to incorporate a number of ranges of indirection.
extern "C" bool random_bool1()
{
return (random()-random()) > 0;
}
extern "C" bool random_bool2()
{
auto boolgen =
make_gen<lengthy int>()
.zip2(make_gen<lengthy int>(),
[](lengthy int i, lengthy int j) { return (i-j) > 0; });
return boolgen.generate();
}
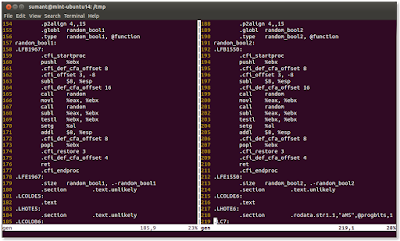
The screenshot under reveals the compiler's meeting output for each the features. The superb truth is that it's precisely an identical! The compiler is ready to see by way of the layers and layers of indirections (invocations of lambdas) and is ready to produce optimum code for the random_bool features. That is fairly a exceptional feat achieved by g++ 5.1 on this case. Maybe it's the identical with different main C++ compilers.
Generator measurement
The efficiency story doesn't finish right here although. Observe that producing a random boolean doesn't want any state. I.e., it's only a perform. Nevertheless, RootRandomGen take one byte as a result of it is a class. Each object in C++ will need to have a novel id. To make sure that's the case, C++ compiler offers minimal doable measurement to every object. As we compose higher-level mills from smaller mills, we're clearly creating objects, which have non-zero sizes. However how a lot reminiscence do they want precisely? What's the measurement of boolgen in random_bool2?
The scale of boolgen is 3 bytes on my machine. The explanation for the state is lambda captures. Each map and zip combinators use lambdas with a number of captures. As higher-level mills are constructed from decrease degree mills, the state provides up. The issue is that in most mills we have seen to this point, there isn't any actual cause to keep up state between two successive calls to the generate perform. I.e, the following worth is totally unrelated to the earlier values. In truth, as we noticed earlier than, the compiler didn't check with any state within the implementation of random_bool2. In fact, for really stateful mills such because the the fibonacci generator, sustaining state from the prior computation is critical.
The build-up of pointless state is kind of quick although. For example, the dimensions of the string generator is whopping 28 bytes! The compiler maintains 28 bytes of state and doesn't serve any apparent goal to the consumer! A generator of printable strings applied as a easy perform would require no persistent state in any respect. As the dimensions of the mills get bigger and bigger, fairly quickly they will not match within the cache line and can begin to degrade efficiency, particularly if really stateful mills are blended with solely accidently stateful mills. I hope compiler writers will determine one thing out about this downside.
This concludes the half 4 within the sequence of Enjoyable with Lambdas: C++14 Type. I hope you loved it. See Dwell Instance.
[ad_2]