Arrays
An array stores a sequence of values that are all of the same type. We want not just to store values but also to be able to quickly access each individual value. The method that we use to refer to individual values in an array is to number and then index them—if we have n values, we think of them as being numbered from 0 to n−1.
Arrays in Java.
Making an array in a Java program involves three distinct steps:
Declare the array name.
Create the array.
Initialize the array values.
We refer to an array element by putting its index in square brackets after the array name: the code a[i] refers to element i of array a[]. For example, the following code makes an array of n numbers of type double, all initialized to 0:
| double[] a; // declare the array a = new double[n]; // create the array for (int i = 0; i < n; i++) // elements are indexed from 0 to n-1 a[i] = 0.0; // initialize all elements to 0.0 |
Typical array-processing code.

Programming with arrays.
Before considering more examples, we consider a number of important characteristics of programming with arrays.
Zero-based indexing. We always refer to the first element of an array a[] as a[0], the second as a[1], and so forth. It might seem more natural to you to refer to the first element as a[1], the second value as a[2], and so forth, but starting the indexing with 0 has some advantages and has emerged as the convention used in most modern programming languages.
Array length. Once we create an array, its length is fixed. You can refer to the length of an a[] in your program with the code a.length.
Default array initialization. For economy in code, we often take advantage of Java’s default array initialization convention. For example, the following statement is equivalent to the four lines of code at the top of this page:
| double[] a = new double[n]; |
The default initial value is 0 for all numeric primitive types and false for type boolean.
Memory representation. When you use new to create an array, Java reserves space in memory for it (and initializes the values). This process is called memory allocation.
Bounds checking. When programming with arrays, you must be careful. It is your responsibility to use legal indices when accessing an array element.
Setting array values at compile time. When we have a small number of literal values that we want to keep in array, we can initialize it by listing the values between curly braces, separated by a comma. For example, we might use the following code in a program that processes playing cards.
| String[] SUITS = { “Clubs”, “Diamonds”, “Hearts”, “Spades” }; String[] RANKS = { “2”, “3”, “4”, “5”, “6”, “7”, “8”, “9”, “10”, “Jack”, “Queen”, “King”, “Ace” }; |
After creating the two arrays, we might use them to print a random card name such as Queen of Clubs, as follows.
| int i = (int) (Math.random() * RANKS.length); int j = (int) (Math.random() * SUITS.length); System.out.println(RANKS[i] + ” of ” + SUITS[j]); |
Setting array values at run time. A more typical situation is when we wish to compute the values to be stored in an array. For example, we might use the following code to initialize an array of length 52 that represents a deck of playing cards, using the arrays RANKS[] and SUITS[] just defined.
| String[] deck = new String[RANKS.length * SUITS.length]; for (int i = 0; i < RANKS.length; i++) for (int j = 0; j < SUITS.length; j++) deck[SUITS.length*i + j] = RANKS[i] + ” of ” + SUITS[j]; System.out.println(RANKS[i] + ” of ” + SUITS[j]); |
Shuffling and sampling.
Now we describe some useful algorithms for rearranging the elements in an array.
Exchange. Frequently, we wish to exchange two values in an array. Continuing our example with playing cards, the following code exchanges the card at position i and the card at position j:
| String temp = deck[i]; deck[i] = deck[j]; deck[j] = temp; |
Shuffling. The following code shuffles our deck of cards:
| int n = deck.length; for (int i = 0; i < n; i++) { int r = i + (int) (Math.random() * (n-i)); String temp = deck[r]; deck[r] = deck[i]; deck[i] = temp; } |
Proceeding from left to right, we pick a random card from deck[i] through deck[n-1] (each card equally likely) and exchange it with deck[i]. This code is more sophisticated than it might seem:
Sampling without replacement. In many situations, we want to draw a random sample from a set such that each member of the set appears at most once in the samplePrecomputed values.
One simple application of arrays is to save values that you have computed, for later use. As an example, suppose that you are writing a program that performs calculations using small values of the harmonic numbers. One easy way to accomplish such a task is to save the values in an array with the following code
| double[] harmonic = new double[n]; for (int i = 1; i < n; i++) harmonic[i] = harmonic[i-1] + 1.0/i; |
and then simply use the code harmonic[i] to refer to any of the values. Precomputing values in this way in an example of a space-time tradeoff: by investing in space (to save the values) we save time (since we do not need to recomputed them). This method is not effective if we need values for huge n, but it is very effective if we need a huge number of values for small n.
Simplifying repetitive code.
As an example of another simple application of arrays, consider the following code fragment, which prints the name of a month given its number (1 for January, 2 for February, and so forth):
| if (m == 1) System.out.println(“Jan”); else if (m == 2) System.out.println(“Feb”); else if (m == 3) System.out.println(“Mar”); else if (m == 4) System.out.println(“Apr”); else if (m == 5) System.out.println(“May”); else if (m == 6) System.out.println(“Jun”); else if (m == 7) System.out.println(“Jul”); else if (m == 8) System.out.println(“Aug”); else if (m == 9) System.out.println(“Sep”); else if (m == 10) System.out.println(“Oct”); else if (m == 11) System.out.println(“Nov”); else if (m == 12) System.out.println(“Dec”); |
We could also use a switch statement, but a much more compact alternative is to use an array of strings consisting of the names of each month:
| String[] MONTHS = { “”, “Jan”, “Feb”, “Mar”, “Apr”, “May”, “Jun”, “Jul”, “Aug”, “Sep”, “Oct”, “Nov”, “Dec” }; … System.out.println(MONTHS[m]); |
This technique would be especially useful if you needed to access the name of a month by its number in several different places in your program. Note that we intentionally waste one slot in the array (element 0) to make MONTHS[1] correspond to January, as required.
Coupon collector.

Suppose that you have a shuffled deck of cards and you turn them face up, one by one. How many cards do you need to turn up before you have seen one of each suit? This is an example of the famous coupon collector problem. In general, suppose that a trading card company issues trading cards with n different possible cards: how many do you have to collect before you have all n possibilities, assuming that each possibility is equally likely for each card that you collect? The prime counting unction π(n) is the number of primes less than or equal to n. For example π(17) = 7 since the first seven primes are 2, 3, 5, 7, 11, 13, and 17
Two-dimensional arrays.
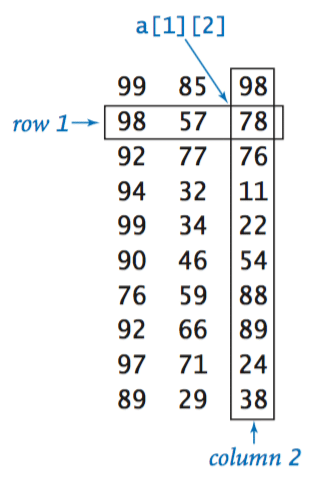
In many applications, a natural way to organize information is to use a table of numbers organized in a rectangle and to refer to rows and columns in the table. The mathematical abstraction corresponding to such tables is a matrix; the corresponding Java construct is a two-dimensional array.
Two-dimensional arrays in Java. To refer to the element in row i and column j of a two-dimensional array a[][], we use the notation a[i][j]; to declare a two-dimensional array, we add another pair of brackets; to create the array, we specify the number of rows followed by the number of columns after the type name (both within brackets), as follows:
| double[][] a = new double[m][n]; |
We refer to such an array as an m-by-n array. By convention, the first dimension is the number of rows and the second dimension is the number of columns.
Default initialization. As with one-dimensional arrays, Java initializes all entries in arrays of numbers to 0 and in arrays of booleans to false. Default initialization of two-dimensional arrays is useful because it masks more code than for one-dimensional arrays. To access each of the elements in a two-dimensional array, we need nested loops:
| double[][] a; a = new double[m][n]; for (int i = 0; i < m; i++) for (int j = 0; j < n; j++) a[i][j] = 0; |
Memory representation. Java represents a two-dimensional array as an array of arrays. A matrix with m rows and n columns is actually an array of length m, each entry of which is an array of length n. In a two-dimensional Java array, we can use the code a[i] to refer to the ith row (which is a one-dimensional array). Enables ragged arrays.
Setting values at compile time. The following code initializes the 11-by-4 array a[][]:
| double[][] a = { { 99.0, 85.0, 98.0, 0.0 }, { 98.0, 57.0, 79.0, 0.0 }, { 92.0, 77.0, 74.0, 0.0 }, { 94.0, 62.0, 81.0, 0.0 }, { 99.0, 94.0, 92.0, 0.0 }, { 80.0, 76.5, 67.0, 0.0 }, { 76.0, 58.5, 90.5, 0.0 }, { 92.0, 66.0, 91.0, 0.0 }, { 97.0, 70.5, 66.5, 0.0 }, { 89.0, 89.5, 81.0, 0.0 }, { 0.0, 0.0, 0.0, 0.0 } }; |
Ragged arrays. There is no requirement that all rows in a two-dimensional array have the same length—an array with rows of nonuniform length is known as a ragged array. The possibility of ragged arrays creates the need for more care in crafting array-processing code. For example, this code prints the contents of a ragged array:
| for (int i = 0; i < a.length; i++) { for (int j = 0; j < a[i].length; j++) { System.out.print(a[i][j] + ” “); } System.out.println(); } |
Multidimensional arrays. The same notation extends to arrays that have any number of dimensions. For instance, we can declare and initialize a three-dimensional array with the code
| double[][][] a = new double[n][n][n]; |
and then refer to an entry with code like a[i][j][k].Matrix operations.

Typical applications in science and engineering involve implementing various mathematical operations with matrix operands. For example, we can add two n-by-n matrices as follows:
| double[][] c = new double[n][n]; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { c[i][j] = a[i][j] + b[i][j]; } } |
Similarly, we can multiply two matrices. Each entry c[i][j] in the product of a[] and b[] is computed by taking the dot product of row i of a[] with column j of b[].
| double[][] c = new double[n][n]; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { for (int k = 0; k < n; k++) { c[i][j] += a[i][k]*b[k][j]; } } } |
