Educating Youngsters Programming – Breadth First Search Algorithm to Compute the Most Variety of Linked Elements in a Directed Graph (Detonate the Most Bombs)

Educating Youngsters Programming: Movies on Information Buildings and Algorithms

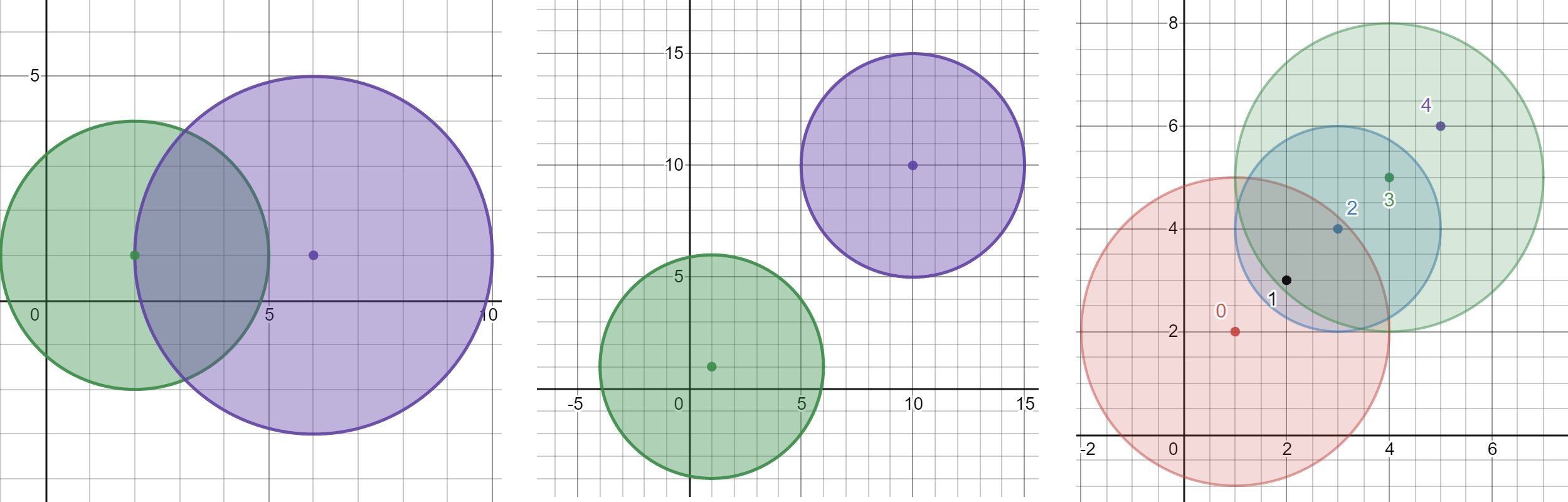
You might be given a listing of bombs. The vary of a bomb is outlined as the realm the place its impact may be felt. This space is within the form of a circle with the middle as the situation of the bomb.

The bombs are represented by a 0-indexed 2D integer array bombs the place bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the situation of the ith bomb, whereas ri denotes the radius of its vary.

You could select to detonate a single bomb. When a bomb is detonated, it can detonate all bombs that lie in its vary. These bombs will additional detonate the bombs that lie of their ranges.

Given the listing of bombs, return the utmost variety of bombs that may be detonated in case you are allowed to detonate just one bomb.

Detonate the Most Bombs

Instance 1:
Enter: bombs = [[2,1,3],[6,1,4]]
Output: 2
Clarification:
The above determine exhibits the positions and ranges of the two bombs.
If we detonate the left bomb, the suitable bomb is not going to be affected.
But when we detonate the suitable bomb, each bombs will probably be detonated.
So the utmost bombs that may be detonated is max(1, 2) = 2.

Instance 2:
Enter: bombs = [[1,1,5],[10,10,5]]
Output: 1
Clarification:
Detonating both bomb is not going to detonate the opposite bomb, so the utmost variety of bombs that may be detonated is 1.

Instance 3:
Enter: bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
Output: 5
Clarification:
The very best bomb to detonate is bomb 0 as a result of:
– Bomb 0 detonates bombs 1 and a pair of. The pink circle denotes the vary of bomb 0.
– Bomb 2 detonates bomb 3. The blue circle denotes the vary of bomb 2.
– Bomb 3 detonates bomb 4. The inexperienced circle denotes the vary of bomb 3.
Thus all 5 bombs are detonated.

Constraints:
1 <= bombs.size <= 100
bombs[i].size == 3
1 <= xi, yi, ri <= 10^5

Breadth First Search Algorithm to Compute the Most Variety of Linked Elements in a Directed Graph (Detonate the Most Bombs)

In final speak (Educating Youngsters Programming – Max Variety of Linked Elements in a Directed Graph (Detonate the Most Bombs) through Recursive Depth First Search Algorithm), we have now used the Depth First Search (DFS) within the method of Recursion to unravel this puzzle. We will additionally use the Breadth First Search (BFS) to traversal the Directed Graph. The opposite components are the identical: developing a directed graph from a listing of the coordinates and their corresponding radius; checking if bomb B may be detonated if we ignite bomb A (if there’s a directed edge from vertex A to vertex B).

The time complexity is O(N^3) – which is identical to DFS strategy. We have to attempt BFS n occasions, and every BFS takes O(N^2) time. Similar area complexity e.g. O(N^2) for the utilization of Adjacency Checklist to retailer the Directed Graph.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Resolution:
    def maximumDetonation(self, bombs: Checklist[List[int]]) -> int:
 
        def f(a, b):
            x1, y1, r1 = a
            x2, y2, _ = b
            return (x1-x2)**2 + (y1-y2) **2 <= r1**2
 
        G = defaultdict(listing)
        n = len(bombs)
        for i in vary(n):
            for j in vary(n):
                if i != j and f(bombs[i], bombs[j]):
                    G[i].append(j)
 
        def bfs(x):
            q = deque([x])
            seen = set([x])
            whereas q:
                c = q.popleft()
                for x in G[c]:
                    if x not in seen:
                        seen.add(x)
                        q.append(x)
            return len(seen)
 
        return max((bfs(i) for i in vary(n)), default=0)

class Resolution:
    def maximumDetonation(self, bombs: Checklist[List[int]]) -> int:

        def f(a, b):
            x1, y1, r1 = a
            x2, y2, _ = b
            return (x1-x2)**2 + (y1-y2) **2 <= r1**2

        G = defaultdict(listing)
        n = len(bombs)
        for i in vary(n):
            for j in vary(n):
                if i != j and f(bombs[i], bombs[j]):
                    G[i].append(j)

        def bfs(x):
            q = deque([x])
            seen = set([x])
            whereas q:
                c = q.popleft()
                for x in G[c]:
                    if x not in seen:
                        seen.add(x)
                        q.append(x)
            return len(seen)

        return max((bfs(i) for i in vary(n)), default=0)

The return worth of the BFS is the variety of the linked vertices aka the bombs that may be detonated on the identical time)

–EOF (The Final Computing & Expertise Weblog) —

GD Star Ranking
loading…

830 phrases
Final Put up: Educating Youngsters Programming – Max Variety of Linked Elements in a Directed Graph (Detonate the Most Bombs) through Recursive Depth First Search Algorithm