Sensible Statistics for Information Scientists

Picture by unsplash

Statistical ideas are used extensively to extract helpful info from information. This text will evaluate important statistical ideas relevant in information science and machine studying. 

A chance distribution reveals how function values are distributed across the imply worth. Utilizing the iris dataset, the chance distributions for the sepal size, sepal width, petal size, and petal width could be generated utilizing the code beneath.

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
import seaborn as sns

iris = sns.load_dataset("iris")
sns.kdeplot(information=iris)
plt.present()

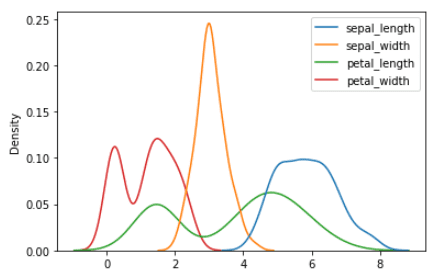
Likelihood distribution of sepal size, sepal width, sepal width, petal size, and petal width | Picture by Writer

Lets now concentrate on the sepal size variable. The chance distribution of the sepal size variable is proven beneath.

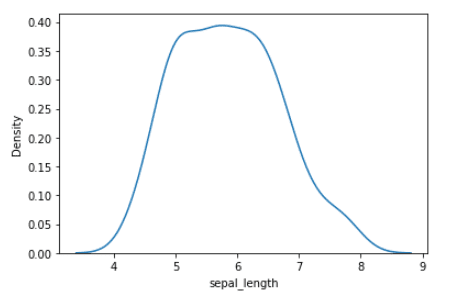
Likelihood distribution of sepal size variable | Picture by Writer

We observe that the chance distribution of the sepal size variable has a single most, therefore it’s unimodal. The worth of the sepal size the place the utmost happens is the mode, which is about 5.8.

A plot of the chance distribution of the petal width variable is proven beneath.

Likelihood distribution of the petal width variable | Picture by Writer

From this plot, we observe that the chance distribution of the petal size variable has 2 maxima, therefore it’s bimodal. The values of the sepal size the place the maxima happens are the mode, that’s at 1.7 and 5.0.

The imply worth is a measure of central tendency. The imply worth for the sepal size variable is obtained as follows:

information = datasets.load_iris().information
sepal_length = information[:,0]
imply = np.imply(sepal_length)
>>> 5.843333333333334

The median worth can also be a measure of central tendency. The median worth is much less vulnerable to the presence of outliers, therefore a extra dependable measure of central tendency, in comparison with the imply worth.  The median worth for the sepal size variable is obtained as follows:

information = datasets.load_iris().information
sepal_length = information[:,0]
np.median(sepal_length)
>>> 5.8

Commonplace deviation is a measure of fluctuations of knowledge values across the imply worth. It’s used to quantify the diploma of uncertainty within the dataset. The usual deviation for the sepal size function is calculated utilizing the code beneath.

information = datasets.load_iris().information
sepal_length = information[:,0]
std = np.std(sepal_length)
>>> 0.8253012917851409

The arrogance interval is the vary of values across the imply. The 65% confidence interval is the vary of values which are one customary deviation from the imply worth. The 95% confidence interval is the vary of values which are two customary deviations from the imply worth. The boxplot beneath reveals the imply worth and 65% confidence interval for the sepal size function.

sns.boxplot(information = iris, y='sepal_length')
plt.present()

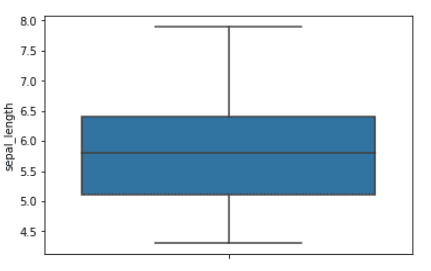
Boxplot for the sepal size function. The blue area signifies the 65% confidence interval | Picture by Writer

Likelihood distributions can be utilized for predictive modeling. The sepal size function solely has 150 information factors. Suppose that we wish to generate extra information factors. Then assuming that the sepal size function is generally distributed, we will generate extra information factors. Within the instance beneath, we generate N = 1000 information factors for the sepal size function.

np.random.seed(10**7)
mu = imply
sigma = std
x = np.random.regular(imply, std, N)
   
num_bins = 50
   
n, bins, patches = plt.hist(x, num_bins, 
                            density = 1, 
                            coloration="inexperienced",
                            alpha = 0.7)
   
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
     np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
  
plt.plot(bins, y, '--', coloration="black")
  
plt.xlabel('sepal size')
plt.ylabel('chance distribution')
  
plt.title('matplotlib.pyplot.hist() perform Examplenn',
          fontweight ="daring")
  
plt.present()

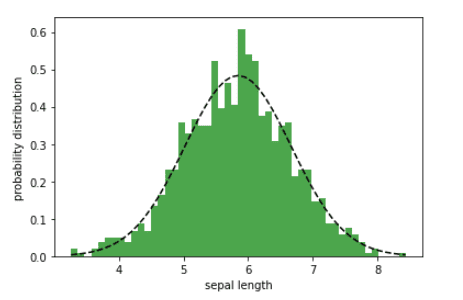
Likelihood distribution of the sepal size width | Picture by Writer

Bayes’ theorem is a vital theorem in statistics and information science. It’s used for evaluating the predictive energy of binary classification algorithms. A easy tutorial on how Bayes’ theorem is utilized in a binary classification algorithm is discovered right here: Bayes’ Theorem in Plain English.

In abstract, we’ve reviewed the important statistical ideas helpful for information science similar to mode, median, imply, customary deviation, chance distributions, regular distribution, and Bayes’ theorem. Anybody desirous about information science should study the basics of statistics.
 
 
Benjamin O. Tayo is a Physicist, Information Science Educator, and Author, in addition to the Proprietor of DataScienceHub. Beforehand, Benjamin was educating Engineering and Physics at U. of Central Oklahoma, Grand Canyon U., and Pittsburgh State U.